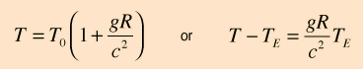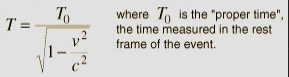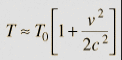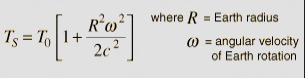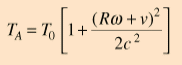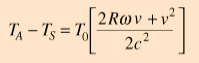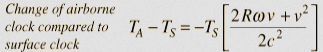The Truth About The Creation
God's Glory, God's Handiwork, God's
Word, The Genesis Account
A Dissertation by Pastor Ed Rice January 2017
Appendix 3: Theory of Relativity and
Atomic
Clocks
Georgia State University's web page opens with the declaration
“Black
holes could decide the future of life on Earth – Think of the
Earth as a flat sheet stretched out and held at the corners, now put
a bowling ball in the middle.” (www.gsu.edu
Nov 2015) They also published this short educational article on the
Hafele and Keating Experiment repeated below in its entirety.
From
http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/airtim.html#c3
accessed 10 Nov 2015
Hafele
and Keating Experiment
"During
October, 1971, four cesium atomic beam clocks were flown on regularly
scheduled commercial jet flights around the world twice, once
eastward and once westward, to test Einstein's theory of relativity
with macroscopic clocks. From the actual flight paths of each trip,
the theory predicted that the flying clocks, compared with reference
clocks at the U.S. Naval Observatory, should have lost 40+/-23
nanoseconds during the eastward trip and should have gained 275+/-21
nanoseconds during the westward trip ... Relative to the atomic time
scale of the U.S. Naval Observatory, the flying clocks lost 59+/-10
nanoseconds during the eastward trip and gained 273+/-7 nanosecond
during the westward trip, where the errors are the corresponding
standard deviations. These results provide an unambiguous empirical
resolution of the famous clock "paradox" with macroscopic
clocks."
J.C.
Hafele and R. E. Keating, Science 177, 166 (1972)
Around
the World
In
1971, experimenters from the U.S. Naval Observatory undertook an
experiment to test time dilation . They made airline flights around
the world in both directions, each circuit taking about three days.
They carried with them four cesium beam atomic clocks. When they
returned and compared their clocks with the clock of the Observatory
in Washington, D.C., they had gained about 0.15 microseconds compared
to the ground based clock.
Eastward
Journey Westward Journey
Predicted
-40 +/- 23 ns + 275 +/- 21 ns
Measured
-59 +/- 10 ns + 273 +/- 7 ns
Around-the-World
Atomic Clocks
In
October 1971, Hafele and Keating flew cesium beam atomic clocks
around the world twice on regularly scheduled commercial airline
flights, once to the East and once to the West. In this experiment,
both gravitational time dilation and kinematic time dilation are
significant - and are in fact of comparable magnitude. Their
predicted and measured time dilation effects were as follows:
Predicted:
Time difference in ns
Eastward Westward
Gravitational
144 +/- 14 179 +/- 18
Kinematic
-184 +/- 18 96 +/- 10
Net
effect -40 +/- 23 275 +/- 21
Observed:
-59 +/- 10 273 +/- 21
Gravitational
Time Shifts
For
small changes in gravitational field associated with changes in
altitude above the Earth, the approximate time dilation expression is
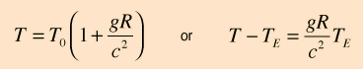
if
a comparison is made between a clock on the Earth's surface (TE) and
one at height h above the surface (T). Hafele and Keating predicted a
time difference of 144 ns on an eastward flight around the world for
which the flight time was 41.2 hours. This corresponds to an average
height of 8900 m, a reasonable flight altitude for a commercial
airline. The time shift is positive (aging faster) for both eastward
and westward flights. The predicted value of 179 ns for the westward
flight of 48.6 hours duration corresponds to an average altitude of
about 9400 meters.
Kinematic
Time Shift Calculation
If the
kinematic
time dilation expression
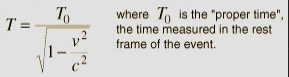
is
expanded in a
binomial expansion, then for small velocities it becomes
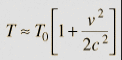
This
expression can
be used to compute the time dilation in the Hafele-Keating experiment
in which an atomic clock was taken aboard an aircraft and compared to
a ground-based clock. The problem encountered with measuring the
difference between a surface clock and one on an aircraft is that
neither location is really an inertial frame. If we take the center
of the earth as an approximation to an inertial frame, then we can
compute the difference between a surface clock and the aircraft
clock. Taking a "proper time" at the earth's center as if
the master clock were there, the time measured by a clock on the
surface would be larger
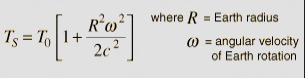
and
that for the
airborne clock would be approximately
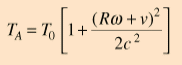
since
to the level
of the approximations used, the height of the aircraft does not
significantly change the radius R. The difference in the times
compared to our hypothetical master clock would then be
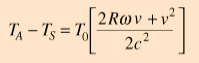
Now
this
relationship is just the reverse of the actual experiment, since we
have assumed that the clock is at the center of the earth, whereas
the actual clocks are in the frames which are moving with respect to
the center. The time difference expression should be valid, but in
comparing the aircraft clock to the surface clock, we should find
that it has fallen behind, so we can model that time difference by
Application
Note
that the
"earth center" time has been replaced by the surface time
in this expression. This is a valid approximation in this case since
the time difference is many orders of magnitude smaller than the time
itself, and this allows us to model the difference between two
measurable times.
Aircraft
Time Dilation
For an
aircraft
flying over the equator, its clocks will show a time shift relative
to a fixed surface clock which can be approximately modeled by the
expression
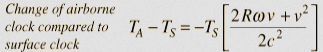
where
the subscripts A and S refer to the aircraft and surface clocks. For
travel eastward, v has a positive sign and the shift will be negative
(aging more slowly). But for a westward flight the time shift is
positive (aging faster) for the aircraft speeds involved. Hafele and
Keating predicted time shifts of -184 ns for an eastward flight
around the world and a shift of +96 for a westward flight.
If you
plug in
numbers for a 48 hour round trip flight at constant speed at the
equator, you get -260 ns and 156 ns for the eastbound and westbound
flights respectively. The predicted values obtained by Hafele and
Keating presumably were based upon detailed measurements of the
speeds, etc.
Hafele
and Keating
are credited with an experimental measurement which confirms time
dilation and matches predictions with an accuracy of about 10%. It
gives an experimental answer to the twin paradox.
Twin
Paradox
The
story is that
one of a pair of twins leaves on a high speed space journey during
which he travels at a large fraction of the speed of light while the
other remains on the Earth. Because of time dilation, time is running
more slowly in the spacecraft as seen by the earthbound twin and the
traveling twin will find that the earthbound twin will be older upon
return from the journey. The common question: Is this real? Would one
twin really be younger?
The
basic question
about whether time dilation is real is settled by the muon
experiment. The clear implication is that the traveling twin would
indeed be younger, but the scenario is complicated by the fact that
the traveling twin must be accelerated up to traveling speed, turned
around, and decelerated again upon return to Earth. Accelerations are
outside the realm of special relativity and require general
relativity.
Despite the experimental difficulties, an experiment on a commercial
airline confirms the existence of a time difference between ground
observers and a reference frame moving with respect to them..
To Continue in this series click the link below:
BIBLIOGRAPHY.
. . 270
www.truthaboutthechrist.com/thetruthaboutthecreation/dissertation_bibliography.html
God's Glory, God's Handiwork, God's Word, The Genesis Account
Series Complete Table of
Contents