5: Algebra's Imaginary Dimension
A short analysis of an ancient craft called Algebra can give important insight about the boundary conditions that produce time warps in God's Universe. It is important to explore the existence of time warps because science-so-called1 is operating under the delusion the it took 168 thousand years for the light of the 1987a supernova to get to planet Earth. The most studied supernova in the universe, is used here as a talking point because the time that light travels through deep space is the only nail holding the age of the universe to the millions mark, yea, now they say billions of years! Understanding boundary conditions, and steps off into other dimensions, is important to those who would understand relativity and warps in the time, space, and matter continuums.
Science-so-called supposes that light entering gargantuan telescopes and coming from the edges of the universe (which they still suppose is infinite and unbounded) took four billion years to get here. They completely disregard the time, space, and matter warps of our focus. The aged craft of Algebra does indeed throw another wrench into their evolutionary machinery; it helps us understand the boundary conditions and multiple dimensions present on the edge of deep space, and in every one of the millions of black-holes in God's unfathomable universe.
Just after God confounded man's language, as recorded in Genesis 11, and just before a son of Eber, named Abram, was called by God to leave Ur of the Chaldees, the Persians began perfecting Algebra. Thus Algebra was up and coming at the same time that Abram was called by God and had his name changed to Abraham. Incidentally, Abram, being a descendant of Eber, generated the nation called Hebrews. Thus Abraham and Algebra were around two thousand years before Christ, and then, almost a thousand years after Christ, the Persians published “The Compendious Book on Calculation by Completion and Balancing” in AD 830. This title, from Baghdad, can be effectively captured in one Arabic word, Algebra. Intelligent man has been striving to balance equations now for 4,000 years, and a key challenge in that balancing effort is called the quadratic equation.
Algebra's Lines and Curves
There are only two pivotal concepts to grapple with in using Algebra to comprehend multidimensional space. They are lines and curves. When one adds two lines together they get another line, but when one multiplies two lines together they get a parabolic curve. That seems simple enough, and it can be aptly illustrated without a lot of mathematical complexity. The meat of this analysis occurs when the parabolic curve is factored back into the two lines which formed it. Some of the curves will factor into lines that are outside of the real world. The real world, for this analysis will be a two-dimensional black board. The boundary where one crosses out of these dimensions and enters into a third dimension will be the heart of this illustration. When one comes off of the blackboard, into the room they enter into the imaginary dimension. When one passes into the wall behind the blackboard they are in that same imaginary dimension. The third dimension, which we can visualize, is not real on our two-dimensional blackboard, and it is thus, called the imaginary dimension.
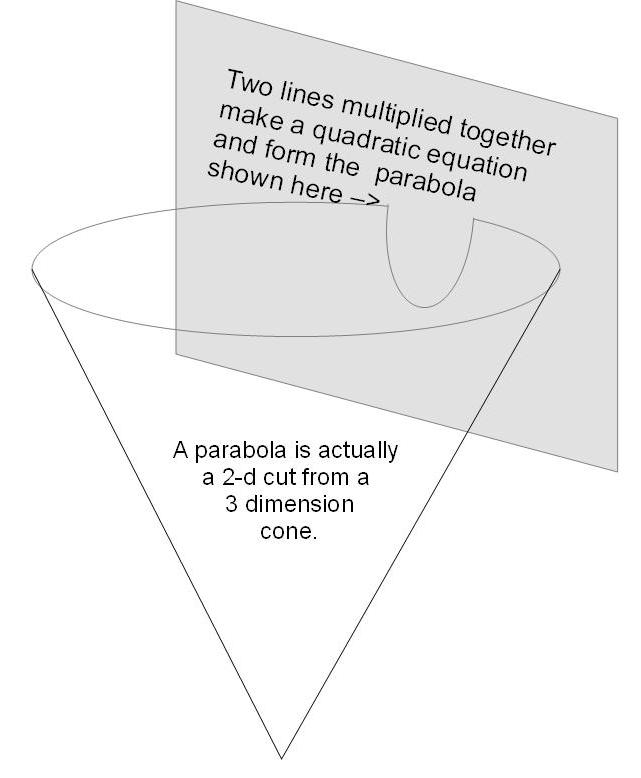
Figure 1 shows that a parabolic curve is in actuality a three-dimensional object, i.e. a cone, that gets captured in a two-dimensional world, i.e. our blackboard. Note that as the cone moves towards or away from the blackboard the shape of the parabolic curve changes. What needs to be applied in this exercise is the ability to visualize that there are similar shapes existing outside of our little three-dimensional world, that bump into us and produce effects that only vaguely get represented in our real world. Beautiful shapes with near-perfect symmetry in an imaginary world produce the warping, curving, and rotations of space and time in our real world. That is abstract and profound.
Two lines multiplying together to form a curve does involve some exotic language, but that language can be helpful in understanding the whole analysis. First consider that this analysis will be done on a two-dimensional plane via our blackboard and chalk. The curve formed from two lines on the blackboard, two lines that multiply
 Figure
1: A cone forms a parabola
Figure
1: A cone forms a parabola
together, is called a “parabola” because it is actually a cone shape which is sliced by the parallel plane of the blackboard. Just like there is an invisible third dimension in our blackboard reality, a dimension that does not fit well in our two-dimensional blackboard's world, so there is a fourth, fifth and sixth dimension to our 3D world. These are the dimensions that do not fit well in our three-dimensional reality. Ergo, this whole analysis is intended to get one used to thinking “outside of the box.” In fact the equation which defines a parabolic curve is called “quadratic” because it is solved (actually “resolved,” or in Algebra of antiquity “balanced”) by the use of the “quadrate,” a word from antiquity meaning square (or box). Armed with this insightful etymology of Algebra let us examine the formation of the parabolic curve.
Linear Algebra consists of lines. Lines on a two-dimensional blackboard can be represented in two variables forever called x and y. The line where Y1 = X + 1 is portrayed in the snapshot of a TI-832 graphing calculator used throughout this analysis. A second line, where Y2 = X + 7 is similarly shown.
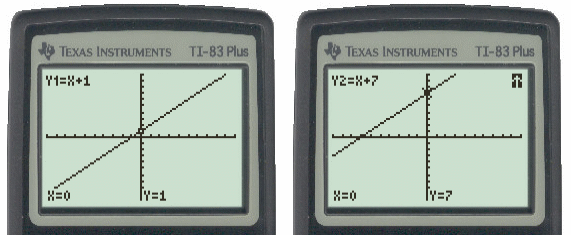 Figure 2: Graph of lines x + 1 and x + 7
Figure 2: Graph of lines x + 1 and x + 7
When these two lines are multiplied together the result is the quadratic equation as follows:
Y3 = Y1 * Y2 = (X + 1) * (X + 7)
= X * (X + 1) + 7 * (X + 1)
= X^2 + 1 X + 7 X + 7
= X^2 + 8 X + 7
The resulting parabolic curve from this quadratic equation is shown below:
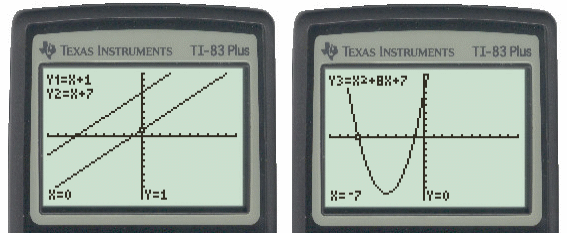 Figure 3: Graph of x + 1 and x + 7 and their resulting parabola
Figure 3: Graph of x + 1 and x + 7 and their resulting parabola
The parabolic curve is actually a cut away two-dimensional view of a conic section, as shown in Figure 1. Picture what happens when stepping the blackboard a bit further away from this cone. This gives another parabolic curve created by multiplying lines Y1 = X + 2 and Y2 = X + 6, where:
Y3 = Y1 * Y2 = (X+2)*(X+6) = X^2 + 8X + 12
Those graphs are shown below:
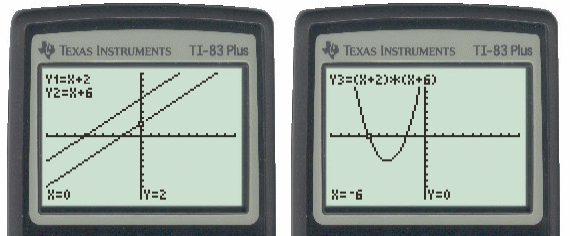 Figure 4: Graph of x + 2 and x + 6 and their
resulting parabola
Figure 4: Graph of x + 2 and x + 6 and their
resulting parabola
Stepping the blackboard even a bit further away from this cone gives another parabolic curve created by multiplying lines Y1 = X + 3 and Y2 = X + 5, where:
Y3 = Y1 * Y2 = (X+3)*(X+5) = X^2 + 8X + 15
Those graphs are shown below:
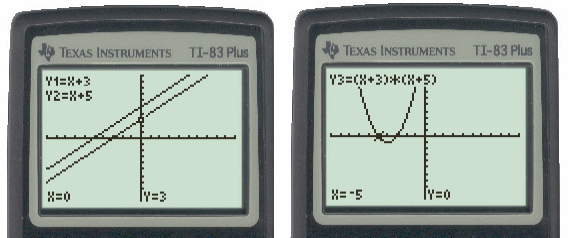 Figure 5: Graph of x + 3 and x + 5 and their
resulting parabola
Figure 5: Graph of x + 3 and x + 5 and their
resulting parabola
Taking the blackboard another step away from this cone, bear with me, this will now get interesting, gives yet another parabolic curve created by multiplying lines Y1 = X + 4 and Y2 = X + 4. These lines are identical and the multiplying them makes a square as shown below:
Y3 = Y1 * Y2 = (X+4)*(X+4) = (X + 4)^2 = X^2 + 8X + 16
Those graphs are shown below:
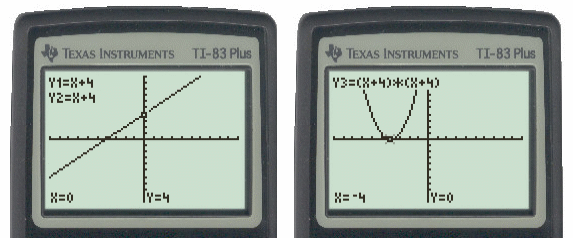 Figure 6: Graph of x + 4 squared and the resulting
parabola
Figure 6: Graph of x + 4 squared and the resulting
parabola
Notice now, at this crucial point of transition, that stepping the blackboard another step away from the cone will show a parabolic curve, however the lines that multiply to form it must transition into the imaginary world. They are still real, they just disappear into an imaginary plane that is not on this two-dimensional blackboard. From their imaginary plane, out of our view, they still multiply together to give a real parabolic curve: a curve that is in our plane and on our blackboard. Two such graphs are shown below:
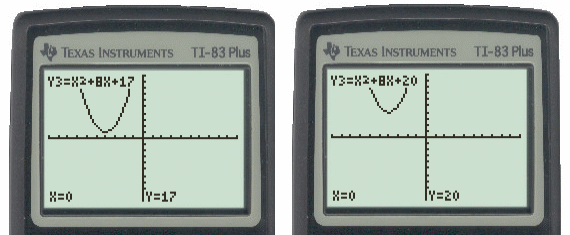 Figure 7: Graph of parabolas from multiplied
imaginary lines.
Figure 7: Graph of parabolas from multiplied
imaginary lines.
Since the TI-83 cannot display all these parabolas on one screen in color the following chart may be helpful: The graph of the pairs of lines which multiply together to form these parabolas (less the last two, of course, which are off in an imaginary plane) are show in the graph below:
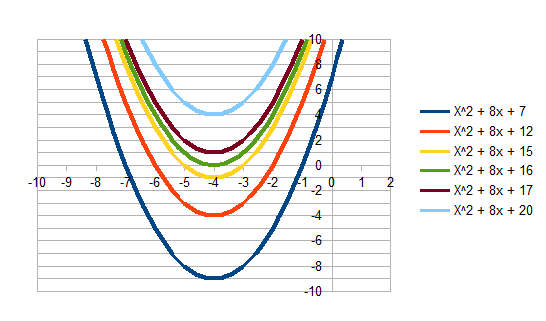 Figure 8: Graphs of the pairs of lines multiplied to form various
parabolas
Figure 8: Graphs of the pairs of lines multiplied to form various
parabolas
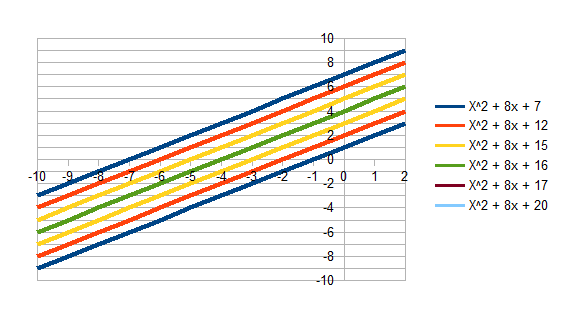 Figure 9: Graphs of the pairs of lines multiplied to form various
parabolas
Figure 9: Graphs of the pairs of lines multiplied to form various
parabolas
The imaginary lines which multiply together to give the last two parabolic curves are as follows:
Y3 = X^2 + 8X + 17 = (X + 4 + √-1 )*(X + 4 - √-1 ) and
Y3 = X^2 + 8X + 20 = (X + 4 + 2√-1 )*(X + 4 - 2√-1 )
These lines, (X + 4 ± √-1 ) and (X + 4 ± 2√-1 ), are calculated from a completion of squares method for solving quadratic equations (the method is formalized in Algebra's famous Quadratic Equation,3 which solves for the roots of a quadratic equation). The term, √-1 , is what makes these lines imaginary. It is normally designated, i, and called imaginary because there is no such value in the real world, i.e. there is no square root of a negative number because there is no number multiplied by itself which could result in a negative number. And yet there you have it, such a term is necessary for the solution of this quadratic equation. Indeed such an imaginary term, in an imaginary dimension, is required in many mathematical applications. And this imaginary dimension, outside of our three-dimensional world, is a mainstay of Albert Einstein's theories of relativity.
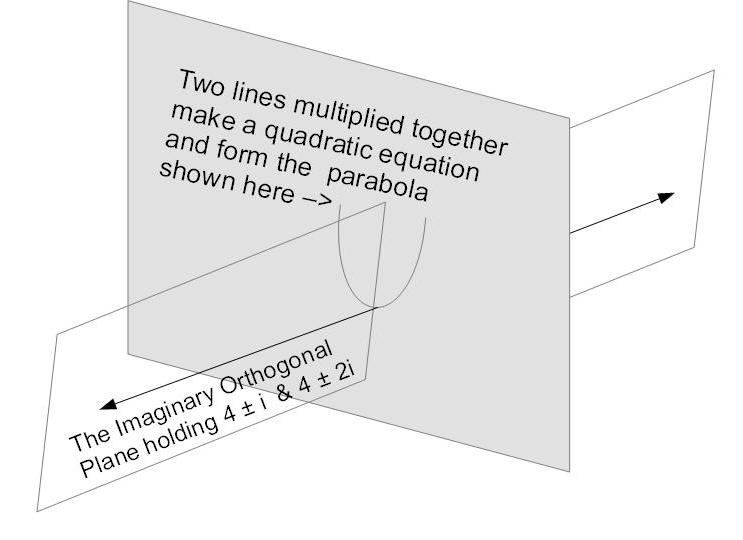 Figure10 : Graphic of a plane orthogonal to the
blackboard.
Figure10 : Graphic of a plane orthogonal to the
blackboard.
Explore this imaginary dimension through the consideration of the imaginary pair of lines which multiply together and come back into our real world as a quadratic equation. First consider the two lines Y = X + 4 ± √-1 = X + 4 ± i . They may be rationalized as existing in two parallel planes, one just in front of, and one just behind, the blackboard which contains the real parabola, Y = X^2 + 8X + 17. The next parabola, Y = X^2 + 8X + 20 can be factored into the two lines, Y = X + 4 ± 2i which may be rationalized as existing in two parallel planes, one just a little further in front, and one just a little further behind, the blackboard.
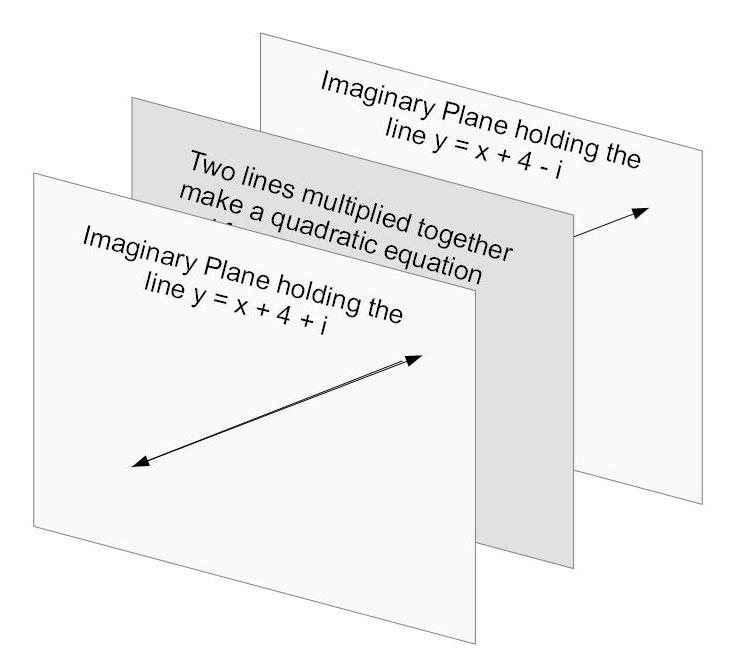 Figure 11: Graphic of the imaginary planes relative
to the blackboard
Figure 11: Graphic of the imaginary planes relative
to the blackboard
One can now visualize the pattern with this sequence of parabolic curves; as they move upward the lines which form them move closer together The lines touch their parabola where it crosses the x axis and y equals zero. When the parabola only touches the x axis at a single point the two lines collide into one. And when the parabola does not touch the x axis, i.e. reaching a point where y equals zero, then the lines move off into an imaginary dimension. The further the vertex of the parabola is from the x axis, the further the two imaginary planes are from the plane of the blackboard.
Analytic Geometry Goes Even Further
Investigating the two-dimensional figures that are formed when a right circular cone is intersected by a plane is called Analytical Geometry. Three-hundred years before Christ the Greek mathematician Menaechmus (380 – 320 BC) discovered “depending how he tilted the plane when it intersected the cone, he formed different shapes at the intersection – beautiful shapes with near-perfect symmetry.”4 The heart of Analytic Geometry is the development of defining equations for all these shapes, but here an overview of their formation will suffice.
In Figure 12 below the concept of a plane cutting a conic section and forming a curve in two-dimensional space is illustrated. In the next figure the types of curves that can be formed is more fully captured. Notice again that the shape that causes the curve is outside of its dimensions, and is thus in an imaginary dimension.
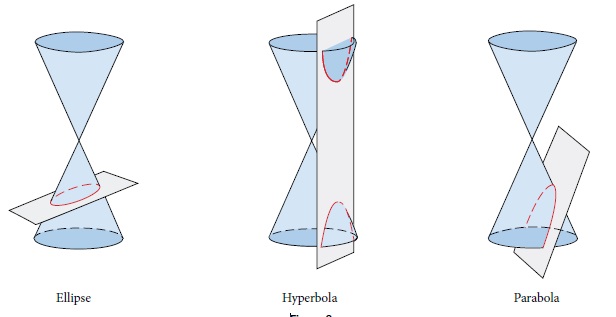 Figure 12 Planes Cutting Conic Sections (OpenStax Precalculus)
Figure 12 Planes Cutting Conic Sections (OpenStax Precalculus)
The four basic two-dimensional curves which are attributed to such conic sections are shown in Figure 13. Conic sections outside of the two-dimensional plane interact to produce effects in the two-dimensional plane.
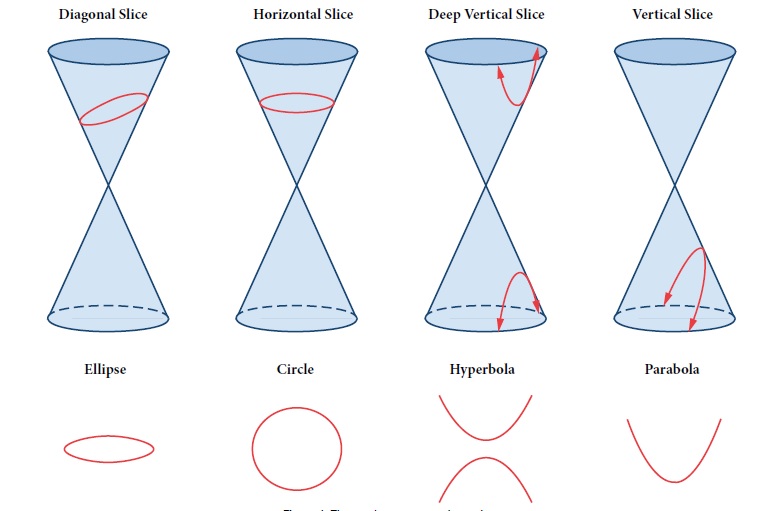 Figure 13 Curves Produced by Conic Sections (OpenStax
Precalculus)
Figure 13 Curves Produced by Conic Sections (OpenStax
Precalculus)
It should be noted that even simple straight lines and points can be generated by conic sections interacting with a two-dimensional plane. These are called degenerate conic sections because they degenerate form a complex form into a very simple two-dimensional form. These are shown in Figure 14.
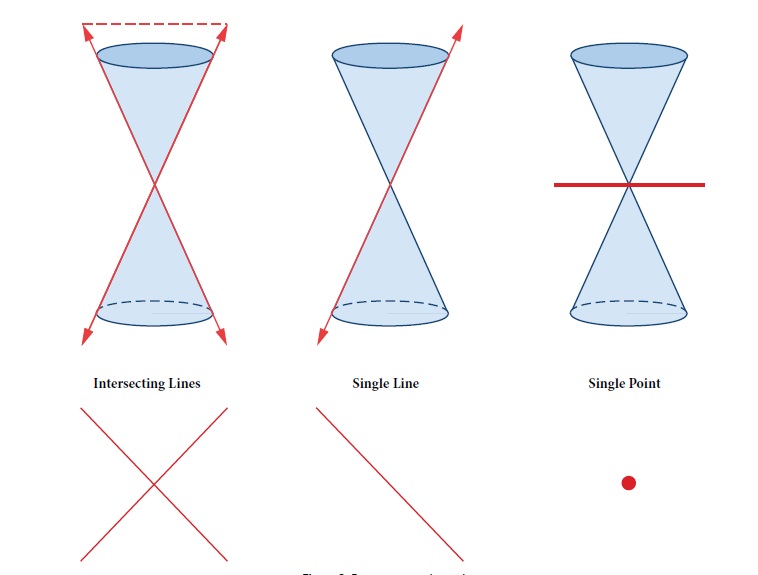 Figure 14 Degenerate Conic Sections, Lines and Points (OpenStax
Precalculus)
Figure 14 Degenerate Conic Sections, Lines and Points (OpenStax
Precalculus)
We need not go any deeper into Analytic Geometry to comprehend that imaginary dimensions outside of our perceived three-dimensional world produce effects within our three-dimensional world. The same way that the dimensions outside of the two-dimensional blackboard produce linear and symmetric geometries on the blackboard, dimensions outside of our three-dimensional world produce relativity effects in our real world. Thus time, space, and matter warping and curving in our world can be conceived and mathematically described by stepping out into imaginary dimensions.
Even More Dimensions
Following this sequence off into the imaginary dimensions, especially comprehending its boundary conditions, empowers an understanding of the other dimensions in the universe. These imaginary dimensions are sometimes fathomed as an imaginary universe, or a parallel universe. The abstract reasoning needed to comprehend time warps and theories of relativity necessitates this journey.
Such a parallel universe occupying imaginary mathematical dimensions is essential for the comprehension and application of Albert Einstein's theories of relativity. In the solution of a simple quadratic equation it is necessary to jump from a two-dimensional plane into a third, albeit imaginary, plane. In a similar manner, operating in a three-dimensional space it will be necessary to jump into an imaginary fourth dimension in order to find solution to our relative reality.
Once one is comfortable with a jump into a fourth dimension of space, it is reasonable to comprehend a fifth. In actuality each of our three dimensions has an orthogonal (at right angles or 90 degrees offset) but mathematically imaginary dimension. And so now there are six dimensions of space. Visualizing these imaginary orthogonal dimensions constructs a parallel universe, where one has, in total, six dimensions, three real and three imaginary. Albert Einstein's general theory of relativity operates in ten dimensions.5 One may have talked with people who were off in another dimension. Albert Einstein had the profound ability to step back into our 3-D real world and teach university students where he had been.
Consider again the solutions to the quadratic equations which were just examined. As the parabola in this view moves up the blackboard, the lines which multiply together to form it move together, until they unite into a single line. At this point the multiplied lines form what is called a square solution. This square solution is what is resolved to find all quadratic solutions, i.e. quadratics use a completion of squares method for this solution.6 When a parabola moves up and above this completed square, the lines move out into an imaginary dimension. They exist out there, they are real out there, and when they multiply together they form a phenomena in our real 3-D world, a phenomena known as a parabola. That is remarkable.
The lines which exist in the imaginary world of mathematics multiply together and produce a phenomena actualized in the real, 3-D, visible, sure-enough, there-it-is, world, the world that one knows and explores. That is almost worth repeating several times.
Once one gets a hold of such a truth, they can enter a realm where everything does not have to be just as it seems. Some “science” must enter into a universe of a greater dimension. Allow, again, Albert Einstein to go there in one of his more basic solutions.
It was Albert Einstein, not Steven Hawking, that originated a concept called “The Theory of Everything.” It began as an effort to understand why gravity and inertia were directly related, i.e. mass responds to gravity with the same set of equations with which it responds to inertia. To comprehend this relationship Albert Einstein had to venture into the imaginary dimension of which I now speak. Upon his return from this parallel universe he gave a simple and yet genius description. It has enlightened many about the need of other dimensions for a more thorough understanding of God's universe.
Gravity might be modeled with a two-dimensional concept existing in a three-dimensional world. Stretch the skin of a balloon over the mouth of a bucket. This elastic will be our two-dimensional world. Now place a large marble in its center, this will cause the elastic to sink in the middle. Take a second, much smaller marble and roll it on the elastic surface around the rim of the bucket. Observe what happens. The rolling ball does not roll in a straight line like inertia would require. Instead it curves and circles around the larger mass in the center of the elastic plane. That is what gravity would require.
Further, as friction decelerates the rolling marble, its inertia decreases and it spirals toward the central marble, just like gravity would draw it in. The genius of this explanation rests on the concept that a two-dimensional problem can be extended into a third dimension for our better understanding. In like manner, understanding the science about our three-dimensional world, can be enhanced when extend into additional dimensions. Understanding that a two-dimensional parabolic curve is in reality a three-dimensional conic section is empowering. And so it goes for expanding from our three dimensions into fourth, fifth and sixth dimensions. One cannot fully comprehend the theories of relativity without this multidimensional perspective.
Why Do We Have To Learn This?
The forever repeated question in Algebra class is, “Why do we have to learn this?” It is often backed with the insight, “My dad said he never used “X”s and “Y”s again in his life.” Arithmetic teaches one to balance their checkbook, Mathematics teaches one to think with abstraction, and Algebra marks ones first step into mathematics. The lazy mind does not deal with abstraction; don't be lazy minded. God wants to renew our diligent minds.
Is it necessary to comprehend a parallel universe to understand the Bible? Unequivocally, no! Understanding the Bible, Genesis to Revelation, requires only comprehension that 1) man is fallen, destitute and unable to repair his fallen estate wherein he is destined to eternal death. 2) “God so loved the world, that he gave his only begotten Son, that whosoever believeth in him should not perish, but have everlasting life.” And 3) “Whosoever shall call on the name of the Lord, shall be saved, … he that hath the son hath life; and he that hath not the Son of God hath not life” (Rom 10:13, 1John 5:12).
When one is saved from eternal death and given God's eternal life, they are quickened, or made alive in a Godly dimension. One is then given eyes to see, and ears to hear. It is no longer “Seeing is believing,” that is only a physical dimension. Now it is “Believing is seeing,” because born-again believers now have God's spiritual dimension born into us. This comprehending of additional dimensions, the exploring of a parallel universe can cause, for those who have eyes to see, a greater depth to God's revelation, and a greater trust that God says what he means and means what he says.
In the same sense, going to Seminary and learning Greek and Hebrew is not necessary for understanding the Bible. Learning the original languages of the Bible does not give one a greater comprehension of what the Bible says, it is the quickening of the Holy Spirit of God that brings any comprehension. So again, learning the original languages does not enable one to believe the Bible or understand the Bible, but it brings a greater depth to God's revelation, and a greater trust in the very words which God used in that revelation. Likewise, understanding the mathematical concepts that make every word of the creation account conceivable brings a greater depth to God's revelation and a greater trust that God says what he means, and means what he says.
Aside from this important spiritual dimension, however, there is still a comprehension of the physical universe which requires the realization of imaginary dimensions and a parallel universe phenomena. Without the comprehension of these dimensions one might simply expect that mass and energy situated out at the edges of the universe behave exactly as they do here in our tiny corner of it all. With such a limitation one will not comprehend any theories of relativity, nor consider that light might project through space without respect of Newtonian physics.
Ignoring all this might lead one to think that a super nova which occurred 168,000 light years away occurred 168,000 years ago. They might emphatically argue that this is just straight science, and those who deny it are brainwashed religionists. They, in ignoring this reality of imaginary dimensions, a parallel universe, and theories of relativity, never have to grapple with the idea that the speed of light might control the tick of the clock, or the tick of a clock might control the speed of light. When they are thus in lock step sync with our Newtonian and Gaussian laws in our local Cartesian coordinate system, they insist that they are the true scientists and any Bible believers are charlatans and liars. Despite their plight, or perhaps because of it, it behooves Christians to step out into the imaginary dimensions, and to comprehend some aspects of Einstein's theories of relativity. It can enhance one's faith, and empower arguments to the general masses deceived by “science-so-called.”
Einstein's Use of Multidimensional Analysis
And so, where have we now come in preparing some basics for Albert Einstein's theories of relativity? Where are we at, knowing Algebra's exposure of an imaginary world of mathematics? Our thesis was that exploring these introductions would open avenues for a very careful belief of every word the LORD gave in his Genesis account. Science-so-called has been exposed as an enemy of believing every word of God. Many atheistic evolutionists may not be purposely, or even consciously pitted against God's revelation. PhDs pursuing their scientific methods have explored the universe with a sincere integrity, but they are restricted from God's truth by barriers of political correctness and Bible ignorance.
Atheistic evolutionists are armed with an a priori refusal to acknowledge our Creator; they refuse to acknowledge the LORD God's revelation of himself in Holy Scripture, supposing instead that the Bible is a man made book. Those contentions are battled on other fronts, here we pursue the theories of relativity, and the reality of deeper dimensions in God's universe. In his youth, as a student of physics, Albert Einstein began attacking the rigidness of scientific law.7 The rigid laws of science were deemed to be omniscient and omnipotent, and Einstein's defiance of such rigidity opened up vistas for his theories of relativity.
Newton's laws of motion and his theory of gravitation were published in his Principia Mathematics in 1687. “Einstein described the Newtonian basis of physics at the end of the nineteenth century as 'eminently fruitful' and 'regarded as final.”8 Albert, the physics student, then wrote much more on Newtonian findings:
It not only gave results for the movements of the heavenly bodies, down to the most minute details, but also furnished a theory of the mechanics of discrete and continuous masses, a simple explanation of the principle of the conservation of energy and a complete and brilliant theory of heat. The explanation of the facts of electrodynamics [the physics of moving electrical charges] within the Newtonian systems was more forced; the least convincing of all, from the very beginning, was the theory of light.”9
As a physicist, Einstein began a retraction of Newton's “Laws,” laws which many regarded as “final.” First in exploring light and its ambiguities, and then exploring gravity and its perfect mystery, Einstein concluded that what Newton regarded as “Scientific Law” was really only “Relative Law.”
At the turn of the nineteenth century the scientific method began to be considered omnipotent and infallible. For the atheistic evolutionist it “evolved” into the omniscient revealer of all truth. In this transition the scientific method underwent a metamorphosis, whereby anybody questioning its veracity was a heretic and worthy of exile or worse. With the scientific method in this infallible, inerrant, exalted position, Albert Einstein, with his theories of relativity, was a particular embarrassment. He rather enjoyed bringing up facts which embarrassed those who thought their laws of science were omnipotent. Although this author also enjoys poking fun at atheistic evolutionists, even as Elijah enjoyed mocking the prophets of Baal (1Kings 18:27), the purpose here is to expose their error so that the Bible believer might not take the false gods to seriously.
The twisted nature of man is revealed when the more obvious the corporate blunder, the more lock step and defiant the corporation becomes. Hans Christian Anderson ingeniously captured that in a short story 190 years ago. In parallel to his story, the finely crafted clothing, fit for the emperor, is woven together by atheistic evolutionists who intertwine an infinite universe, with a Random Chance Creator, all lased into an unbounded cosmos. Indeed the Emperor has no clothes, but if one stands up and says that out loud, all the scientists-so-called point them out and call them fools. They insist that “Random Chance” is their sole creator. Albert Einstein pointed to their omniscient Newtonian laws and said, “There are some things that they do not know!”
The Bible believer can coexist with Einstein and algebra, in a bounded universe. God's Word is in perfect harmony with math and science, and blessed is the man who puts his trust therein. God says what he means, and means what he says. The existence of the black-hole, the general theory of relativity, and the bounded universe, these three profound concepts merge and enlighten God's declaration about his Only Begotten Son, “In the beginning was the Word, and the Word was with God, and the Word was God. The same was in the beginning with God. All things were made by him; and without him was not any thing made that was made. In him was life; and the life was the light of men” (John 1:1-4), and again “Thou art worthy, O Lord, to receive glory and honour and power: for thou hast created all things, and for thy pleasure they are and were created” (Rev 4:11).
Some readers may have just taken their first step deep into the world of abstract reasoning. Comprehending that there are unknown, imaginary dimensions to God's universe is a big step for our finite minds. Such abstraction is normally accompanied by years of training in the higher mathematics that substantiates multidimensional analysis. Such a condensed version was herein attempted because understanding where Albert Einstein went to develop his theories of relativity is helpful in seeing, or at least glimpsing into, the very complex world where time, space, and matter might envelope each other and warp what is otherwise a uniform continuum. Mathematically then, the three dimensions of space and one dimension of time must needs expand into ten dimensions of the universe. Albert Einstein's general theory of relativity transitions the mathematician into that expansion. Before pursuing a leap into Albert Einstein's theories of relativity, however, consider how the added dimension might improve our own cognizance of God's creation.
A Christians use of Multidimensional Analysis
The believer who knows that "All scripture is given by inspiration of God, and is profitable for doctrine, for reproof, for correction, for instruction in righteousness: That the man of God may be perfect, throughly furnished unto all good works" (2Tim 3:16-17), that, "The prophecy came not in old time by the will of man: but holy men of God spake as they were moved by the Holy Ghost" (2Pet 1:21), and that, "The words of the LORD are pure words: as silver tried in a furnace of earth, purified seven times" (Psalm 12:6), knows also that God says what he means, and means what he says.
God, in his Word, gives us his steps in the creation of the universe. He says it was once without form and void and darkness was on the face of the deep. A believer trusts God's words, and can believe without complex abstraction or Albert Einstein's theories. But comprehending the harmony of it all helps one grasp the exactness of God's wordings. An appreciation of that exactness might hinder the tendency to read things between the lines. One thereby strengthens the truth that God says what he means, and leaves no spaces between his words, his words are clear, his days are days, and his thousand years are thousand years. Such clarity comes into better focus when one comprehends that things are not always as they seem in our little three-dimensional world.
When one understands that there are more dimensions to the God's universe than our three little dimensions of space and one continuous dimension of time there is more room for angels moving about, for spiritual insights, and our own transformation in the twinkling of an eye. Things said by an infinite God become more conceivable to the finite mind because of the added dimensions that we can comprehend, but not really understand. The unbelievable, some how becomes a little more believable when we do not restrict God to our world. There are dimensions which we cannot see and they effect the dimensions that we live in. Thus a Red Sea dividing does not take a mighty wind, manna and quail from heaven does not require grain and birds of “natural” means.
One need not be a mathematician to marvel in the multidimensional truths nor explore other dimensions. The believer of God's perfect revelation of all things under heaven can, all the more, marvel in the depths and exactness of his Holy Bible. Romans 11:33 says, “O the depth of the riches both of the wisdom and knowledge of God! how unsearchable are his judgments, and his ways past finding out!” The unregenerate, living in a random chance universe that is evolving into a higher order by some sort of survival of the fittest myth, must shrink into the corner of his library and hide a math book away amongst all his buried "scientific" journals, while he insists that the Emperor is wearing fine clothes. Random chance cannot account for all this wonder in a billion years.
But the believer who understands that there are more dimensions to the universe than what we see knows that, “faith is the substance of things hoped for, the evidence of things not seen,” and that “through faith we understand that the worlds were framed by the word of God, so that things which are seen were not made of things which do appear” (Heb 11:1,3). That believer is better equipped to believe every word of God.
1
This title is derived from 1Timothy 6:20 "O Timothy, keep that
which is committed to thy trust, avoiding profane and vain
babblings, and oppositions of science falsely so called:"
2
TI-83 is the registered trademark of Texas Instruments Incorporated,
copyright 1995-2014
3
The Quadratic Equation is X1&2 = (-b ± √b^2
-4ac )/(2a), where Y = a X^2 + b X + c
4
Jay Abramson, Precalculus,
(Houston: OpenStax College, Rice University,
https://openstax.org/subjects/math,
2015), 863
5
The superscripts in Einstein's general theory of relativity (Gm
n = …)
represent the four dimensions
of space-time (x, y, z, t)
multiplied to form 16 dimensions, however eliminating some repeated
equations results in his 10 dimensions eauation.
6
The famous Quadratic Equation, xi = (- b ±
√
b^2 – 4 a c )
/ (2 a) , used and loved by Algebra students everywhere, is nothing
more than a formulation of the completion of squares method.
7
Andrew Robinson, Einstein: A Hundred Years of Relativity
(Prinston University Press,
2015), 21.
8
Ibid.
9
Ibid.